Informationstheorie

(Andrea Zimmer)

Die Informationstheorie behandelt Probleme der Entstehung, Speicherung, Umwandlung und Übermittlung von Information.

1. Information

1.1 Information und Struktur

Elemente können durch Verknüpfungsoperationen in eine Struktur gebracht werden.

z.B. Menge M = {E;D;L;I}

EDLI

LEID

LIED

Man kann erkennen, dass Elemente mehrere Strukturen annehmen können. Genauso ist es möglich, gleiche Strukturen auf verschiedene Elemente anzuwenden.

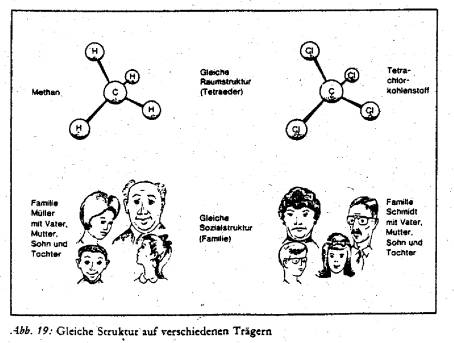
Diese Strukturen sind Träger bestimmter Information.

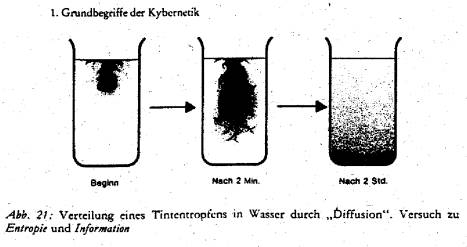
Durch Diffusion geht spezifische Struktur(Information) verloren.

Homogenität (Gleichverteilung) ist der wahrscheinlichste Zustand der Materie.

Die Entropie ist als Maß der Gleichverteilung definiert.
Also wurde die Informationsmenge I als negative Entropie definiert.

1.2 Quantitative Bestimmung der Informationsmenge

Da der einzige quantitativ fassbare Begriff die Wahrscheinlichkeit ist, definiert als:

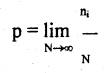
mit n_i/N als relative Häufigkeit

ist es sinnvoll, die Informationsmenge I als eine Funktion von p zu definieren.

(ld ist der Logarithmus zur Basis 2)

wobei bit die Einheit der Informationsmenge im dualen System ist.

Bei einem quantitativen Vergleich von Informationen spielt der Begriff Redundanz eine wichtige Rolle.

Abb. 34: Die Information der 36 weißen Nachbarfelder dient als Redundanz (R=36 bit) zur Kontrastierung und damit zur semantischen Sicherung der Bedeutung „F“

Unter Redundanz versteht man die Differenz zwischen einer gebebenen Informationsmenge und derjenigen, die als Träger einer bestimmten Semantik mindestens erforderlich ist.

1.3 Shannonrische Formel

Beim quantitativen Vergleich von Nachrichtensystemen, treten aber in der Regel Zeichen mit unterschiedlichen Wahrscheinlichkeiten auf. Deshalb ist die Ermittlung des mittleren Informationsgehalts pro Zeichen nötig:

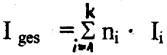
mit I_i: Informationsgehalt des Zeichen

n_i: absolute Häufigkeit

Dann gilt für den mittleren Informationsgehalt I_m

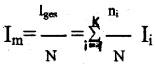
aus 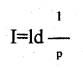und

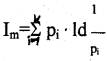
2. Informationsübertragung

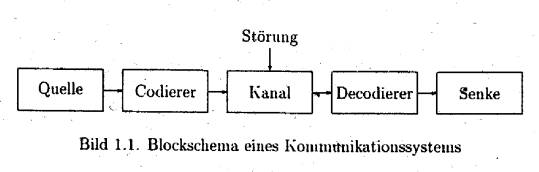
2.1

Die tragende Idee der Information ist, dass die Nachricht der Quelle aus Wörter besteht, die ihrerseits aus Buchstaben des Quellenalphabets X:={a; b ;c;.........z} bestehen. Diese können dann in die Wörter des Codealphabet Y:={0;1} übersetzt werden. Damit ist Telekommunikation äquivalent dem Erzeugen , Senden und Empfangen von Bits ist. So kann also die Informationsübertragung in zwei Probleme aufgeteilt werden:

- Representation der Ausgangssignale der Quelle durch binäre Symbole (Quellenkodierung)

- Übertragen von binären Zufallsfolgen über den Kanal (Kanalkodierung)

Quellencodierungs-Theorem

Jede Quelle kann mit R bit pro Zeiteinheit dargestellt werden. Sie ist äquivalent einer anderen Quelle, die R zufällig erzeugt und gleichwahrscheinliche Bits/Zeiteinheit aussendet.

Kanalcodierungs-Theorem

Der Kanal ist über seine Kapazität C so bestimmt, dass R zufällig gewählte Bits/Zeiteinheit übertragen werden können.

Shannon: Die Informationscodierung ist wichtiger als das Signalstörverhältnis.

Unter Informationscodierung versteht man lange Informationssequenzen, damit jedes Informationsbit Einfluss auf die anderen mitgesendeten Bits hat.

2.2 Mehrbenutzerkommunikation

Telekommunikation besteht größtenteils nicht als Monolog, sondern vielmehr als Mehranwenderkommunikationssystem.

2.3. Kryptologie

Kryptologie dient dem Schutz der Information bei der Übertragung.

Zur Geheimhaltung und Authentizitätssicherung werden Chiffriersysteme benutzt.

3. Sonstige Anwendungen:

Biologie: Artenbestimmung

Informationsmengen von DNS und Polypeptitketten

Steuerungssysteme: Maschinenbau und Robotertechnik

Psychologie: Informationsverarbeitung im Gehirn

Lernforschung

Quellenverzeichnis:

Kybernetik und Biologie – Gerhard Schäfer

Informationstheorie – Rolf Johannesson

Einrührung in die Informationstheorie – Klaus-Dieter Hofmann